Kaveh Pahlevan
Planetary Scientist

Home | Lunar Origin | Atmospheres | Tidal History | Publications | Contact
 
The circumterrestrial disk from which the Moon is thought to have accreted, like Saturn's rings, is expected to relax to the equatorial plane of the proto-Earth on a timescale short relative to its evolutionary timescale. Lunar accretion from such an equatorial disk is expected to initiate the Moon on an orbit inclined by ≈1° from the Earth's equator plane [1,2]. Tidal evolution calculations suggest that for every degree of primordial inclination to the Earth's equator plane, the current lunar orbit should exhibit half a degree of inclination to the Earth's orbital (ecliptic) plane [3,4]. Hence, the order of magnitude disrepancy between the current value of the lunar inclination (≈5°) and expectations from the theory of lunar accretion (≈0.5°) has become known as the lunar inclination problem. I recently developed a new solution to this long-standing problem [5] that was picked up by the press.

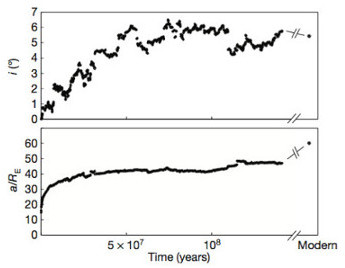
Excitation of the Lunar Inclination
After the giant impact and lunar accretion at ~5-6 Earth radii [6], the Moon undergoes a rapid outward orbital expansion driven by tidal dissipation in the Earth. The rapidity of this early evolution is significant because it drives the system to a separation of 20-40 Earth radii in several million years, while remnant planetesimals from the planet formation epoch persist. Hence, the earliest tidal evolution of the Earth-Moon (EM) system takes place in the presence of heliocentric interlopers. To calculate the effects of these interlopers on the early EM system, we have developed a model of early tidal evolution modulated with gravitational encounters with massive planetesimals. We find that interaction with a small amount of mass can reproduce the modern ≈5° inclination of the lunar orbit.

 Early evolution of the EM system subject to gravitational encounters with planetesimals. The lunar orbit rapidly expands to a separation of 20-40 Earth radii (bottom panel), and experiences a cumulative increase in the orbital inclination (top panel). In this simulation, accretion of 0.0075 Earth masses to Earth after lunar formation reproduces the inclination observed in the modern EM system. From (Pahlevan and Morbidelli, 2015)

Discrimination from Earlier Models
Prior models of the origin of the lunar inclination invoke either a resonance in the Sun-Earth-Moon system [7] or a resonance between the newly accreted Moon and the remnant proto-lunar disk [8]. Importantly, both these proposed mechanisms excite the lunar inclination at very early times (a < 10 Earth radii), while the newly developed collisionless excitation mechanism generally occurs much later (a > 30 Earth radii). Such a clear distinction between the time of excitation between the proposed mechanisms permits discrimination between the models.

It has recently been shown that as the early Moon approaches the Cassini state transition, starting at ~20 Earth radii, obliquity tides in the lunar magma ocean cause the lunar inclination to damp [9]. Hence, either early tidal evolution was so slow that the lunar magma ocean crystallized before reaching ~20 Earth radii and early lunar inclination was preserved, or the early orbital expansion was rapid and any early-acquired (a < 10 Earth radii) lunar inclination was damped, being subsequently excited via collisionless encounters. Determining the dissipation properties of the post-giant-impact Earth [10] can therefore discriminate between the inclination excitation mechanisms proposed to date.

References
  1. Ida, S., Canup, R., Stewart, G. (1997) Lunar accretion from an impact-generated disk, Nature 389, 353-357.
  2. Kokubo, E., Ida, S., Makino, J. (2000) Evolution of a Circumterrestrial Disk and Formation of a Single Moon, Icarus 148, 419-436.
  3. Goldreich, P. (1966) History of the Lunar Orbit, Reviews of Geophysics 4 411-439.
  4. Mignard, F. (1981) The lunar orbit revisited, III. Moon Planets 24 189-207 (1981).
  5. Pahlevan, K., Morbidelli, A. (2015) Collisionless encounters and the origin of the lunar inclination, Nature 527 492-494 link News and Views: The Moon's tilt for gold link Press: Scientists Link Moon's Tilt and Earth's Gold link
  6. Salmon, J., Canup, R. (2012) Lunar accretion from a Roche-interior fluid disk, The Astrophysical Journal 760 1-18.
  7. Touma, J., Wisdom, J. (1998) Resonances in the early evolution of the Earth-Moon system. Astronomical Journal 115 1653-1663.
  8. Ward, W.R., Canup, R.M. (2000) Origin of the Moon's orbital inclination from resonant disk interactions, Nature 403 741-743.
  9. Chen, E., Nimmo, F. (2016) Tidal dissipation in the lunar magma ocean and its effect on the early evolution of the Earth-Moon system, Icarus 275 132-142.
  10. Zahnle, K. et al. (2015) The tethered Moon, Earth and Planetary Science Letters 427 74-82.